What is an Algorithm?
An algorithm is a predefined sequence of steps designed to solve a specific problem or perform a task efficiently. Algorithms are found everywhere—from daily activities like making coffee and solving a Rubik’s cube to complex computer applications such as Google Search, social media platforms, and e-commerce websites.
From brushing your teeth in the morning to following a bedtime routine at night, algorithms guide our actions. In mathematics, formulas and equations serve as algorithms, while in programming, algorithms define how input is processed to generate the desired output.
Algorithms can be represented in multiple ways, including:
- Plain English descriptions
- Flowcharts
- Programming languages
Algorithm:
For Examples let us see an Algorithm to find the greatest of three numbers.
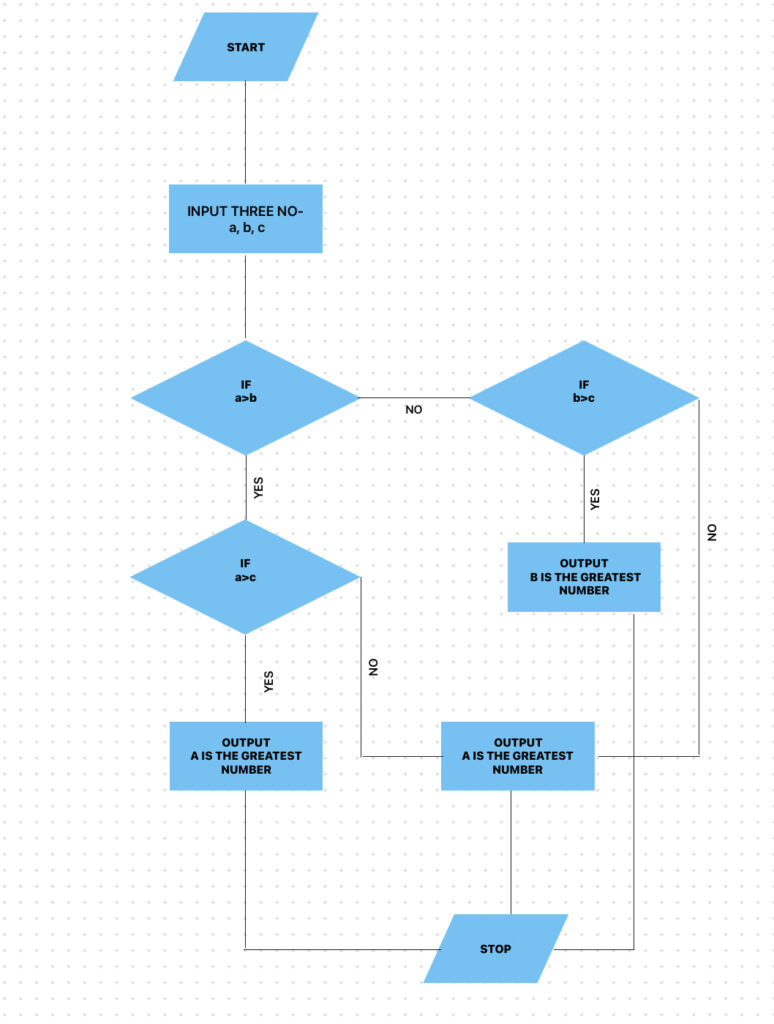
Start
Input three numbers A, B & C.
Check IF A>B
IF Yes
{Check IF A>C
IF Yes
Output A is greatest
IF No
Output C is gratest }
IF No
{Check IF B>C
IF Yes
Output B is greatest
IF No
Output C Is greatest }
Stop
Flowchart of the above algorithm-
Key Characteristics of an Algorithm
For a process to be classified as an algorithm, it must meet certain fundamental properties:
- Input: Accepts zero or more inputs.
- Output: Produces at least one output (result).
- Definiteness: Each step must be well-defined and unambiguous.
- Finiteness: The algorithm must terminate after a finite number of steps.
- Effectiveness: Each step should be simple enough to be executed in a reasonable time.
Real-World Example: Making a Cup of Tea as an Algorithm
A simple, everyday task like making tea can be broken down into an algorithm:
- Boil water to 100°C.
- Add tea leaves to the boiling water.
- Allow the tea to steep for 3-5 minutes.
- Add sugar and milk (if needed).
- Strain the tea and serve in a cup.
This sequence meets all the algorithmic requirements: clearly defined steps, a well-defined outcome, and a finite number of steps.
Why Are Algorithms Important?
Algorithms are essential because they:
✅ Automate repetitive tasks – Used in robotics, AI, and software automation.
✅ Improve efficiency – Optimized algorithms reduce computation time and resource usage.
✅ Enable decision-making – Used in AI, finance, healthcare, and cybersecurity.
✅ Enhance scalability – Algorithms help systems handle large-scale data efficiently.
✅ Power modern technology – They are the foundation of search engines, social media, and self-driving cars.
Types of Algorithms and Their Applications
1. Brute Force Algorithm
A brute force algorithm systematically tries all possible solutions until it finds the correct one.
🔹 Applications:
- Linear Search – Checks each element one by one.
- Password Cracking – Attempts all possible password combinations.
- Combinatorial Problems – Finds the best path in a maze by testing all possible routes.
🔹 Efficiency Concern:
- Works for small datasets but is highly inefficient for large problems.
- Time Complexity:
\(( O(n) )\) in most cases.
2. Greedy Algorithm
A greedy algorithm makes the best immediate choice at each step, hoping it leads to the optimal solution.
🔹 Applications:
- Coin Change Problem – Picks the highest denomination first.
- Dijkstra’s Algorithm – Finds the shortest path in a graph.
- Huffman Coding – Used in data compression techniques.
🔹 Efficiency Concern:
- Does not always guarantee the best global solution.
- Time Complexity: ( O(n) ) in simple cases.
3. Recursive Algorithm
A recursive algorithm solves a problem by breaking it down into smaller subproblems of the same type.
🔹 Applications:
- Factorial Calculation:
\(( n! = n \times (n – 1)! )\) - Fibonacci Series: \(( F(n) = F(n – 1) + F(n – 2) )\)
- Tower of Hanoi Puzzle – Moving disks between rods in a systematic way.
🔹 Efficiency Concern:
- Can lead to excessive memory usage if not optimized.
- Time Complexity:
\( O(n) \) for simple recursion,\(( O(2^n) )\) for Fibonacci without optimization.
4. Divide and Conquer Algorithm
This approach divides a problem into smaller subproblems, solves them independently, and then combines the results.
🔹 Applications:
- Merge Sort – Splits an array, sorts halves, and merges them.
- Binary Search – Searches for an element in a sorted array efficiently.
- QuickSort – Divides and sorts using pivot elements.
🔹 Efficiency Benefit:
- Time Complexity:
\( O(n \log n) \) , making it highly efficient for sorting and searching.
5. Dynamic Programming (DP) Algorithm
Dynamic programming solves a problem by storing previously computed results to avoid redundant calculations.
🔹 Applications:
- Fibonacci Sequence (Optimized Approach) – Stores previous values to avoid recomputation.
- Knapsack Problem – Used in resource allocation and decision-making.
- Shortest Path Algorithms – Floyd-Warshall algorithm for optimized route calculations.
🔹 Efficiency Benefit:
- Reduces computation time significantly.
- Time Complexity:
\( O(n) \) with memoization.
6. Randomized Algorithm
This algorithm introduces randomness at some steps to optimize performance or reduce time complexity.
🔹 Applications:
- Randomized QuickSort – Selects a random pivot for sorting.
- Monte Carlo Simulations – Used in AI, finance, and probability estimations.
- Cryptographic Key Generation – Ensures security in encryption methods.
🔹 Efficiency Concern:
- May not always guarantee the most accurate result.
- Time Complexity:
- Best-case:
\( O(n \log n) \). - Worst-case:
\( O(n^2) \) (rare).
Algorithm Complexity and Performance Analysis
Algorithm efficiency is measured using Big-O notation, which describes how execution time increases with input size.
\( O(1) \) (Constant Time): Execution time remains the same regardless of input size. Example: Accessing an element in an array.\( O(\log n) \) (Logarithmic Time): Execution time grows logarithmically. Example: Binary Search.\( O(n) \) (Linear Time): Time increases proportionally to input size. Example: Linear Search.\( O(n^2) \) (Quadratic Time): Performance decreases rapidly with large inputs. Example: Bubble Sort.- \( O(2^n) \) (Exponential Time): Solving large inputs becomes practically impossible. Example: Recursive Fibonacci.
Understanding algorithm complexity helps in choosing the right approach for problem-solving.
Conclusion: Why Algorithms Matter
Algorithms are the building blocks of modern computing, enabling:
✔ Automation – Powering AI, robotics, and decision-making systems.
✔ Optimization – Improving speed and efficiency.
✔ Scalability – Handling large-scale data processing.
✔ Innovation – Driving advancements in technology and science.
From Google search rankings to self-driving cars, algorithms shape the world around us. Understanding them is essential for anyone in computer science, data science, or AI development.
Next Steps: How to Learn Algorithms?
1️⃣ Master fundamental algorithms – Sorting, searching, recursion.
2️⃣ Learn data structures – Arrays, linked lists, trees, graphs.
3️⃣ Practice coding problems on platforms like LeetCode, CodeChef, HackerRank.
4️⃣ Explore real-world applications – AI, machine learning, cryptography.
💬 Which algorithm do you find most useful? Share your thoughts in the comments!